What is Standard Deviation?

As defined, standard deviation “provides a statistical measure of historical investment return volatility and sets forth a distribution of the ranges of probable outcomes. In investing, measuring the standard deviation of returns shows the extent to which returns (daily, monthly, or annual) are distributed around the average return, estimating a range of probable outcomes, and establishing a likely framework of risk and return trade-offs.”  Ok, that all sounds good, but what does it mean to me as an investor?

Standard deviation is a measure of how much an investment’s returns can vary from its average return. To investors, it is a measure of return volatility which provides a precise measure of how varied an investment’s returns have been over a particular period.  Return volatility, as measured by standard deviation, is the risk that an investment will not meet its expected return for a period. Now, we are getting somewhere.  The smaller an investment’s standard deviation, the less volatile or risky it is perceived to be.  The larger the standard deviation, the more scattered the return outcomes, and an investment is considered to be riskier.  As a measure of investment return volatility, standard deviation can help determine the risk that an investor might take on when purchasing a stock, ETF, or mutual fund.

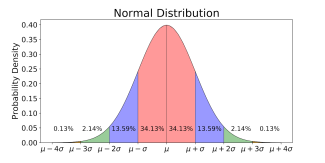
Historical investment returns can be graphed on a normal distribution curve (shape of a bell) in which the mean or average value of returns determines the location of the center of the bell, and the standard deviation determines the width of the bell. When the standard deviation is large (indicating a broad range of outcomes), the bell is short and wide; when the standard deviation is small (indicating a narrow range of outcomes), the bell is tall and thin. In mathematical terms, standard deviation is the square root of the variance, which is defined as “a measurement of the dispersion between numbers in a data set and is calculated by considering the differences between each number in the set and the mean or average value.”

To put these concepts to work, let’s consider the past five-year investment returns of the stock of Company ABC (10%, 8%, 9%, 11% and 12%) and the stock of Company XYZ (20%, 0%, -10%, 10% and 30%), both of which are US large cap companies operating in the same industry sector.   The average return (or mean) of 10% is the same for both ABC and XYZ for the five-year period. The standard deviation, however, is quite different. For ABC the standard deviation is 1.4% and for XYZ it is 14.1%. Our interpretation of the bell curve then tells us that for ABC, in 68.26% of the time its investment returns will be within one standard deviation of the mean or will fall between +8.6% and +11.4%.  In contrast, with XYZ expected returns within one standard deviation of the mean will present a much larger range falling between -4.1% and +24.1%.  So, in the context of this example, if an expected return of 10% meets my investing criteria, then ABC is the less risky and better choice than XYZ.  Which stock would you select?  Company A with its more predictable expected return or Company XYZ which will get you to the same place, but adds some excitement along the way?